Support Forum / Форум поддержки

Another subject of Rosetta's tasks: Please post it on Rosetta if you can

You're a coding wild man! Looks great.

Yes, looks really great!

I have changed the code to the polar form, which is more in accordance to the task description and it reflects SmartBasic's strength with complex numbers. The screenshot has also been adapted. The spiral turns now counterclockwise as to be expected with polar coordinates.

There is a mistake in Wikipedia on the "Archimedian Spiral'. In the equation r=a+b*phi it states that the parameter 'a' turns the spiral.
That is not correct. Parameter 'a' determines the starting point of the spiral.
I have changed the relevant comment in the code accordingly and made some other (minor) changes.

I found this quote in the Wikipedia entry interesting.

Virtually all static spirals appearing in nature are logarithmic spirals, not Archimedean ones.

I'm hoping, Dutchman, that you will also write a version of a logarithmic spiral.

I tried this code out and I only get 1/2 of the first loop.

Is that due to the issue with the a parameter?

How do I fix. (I do have the logarithmic spiral program, but the one pictured below is different.

George.

Dutchman wrote:Another subject of Rosetta's tasks:

Code: Select all

'Archimedean spiral, in polar coordinates
'by Dutchman, december 2016
/*
In polar coordinates (r,phi) the spiral can be described 
by the equation r=a+b*phi with real numbers a and b.
Parameter a determines the starting point,
while b controls the distance between successive turnings.
*/
' --- constants
dphi=0.1 ' angular increment
a=0 ' starting point on real axis
b=100' amplitude parameter
GET SCREEN SIZE sw,sh
x0=sw/2 ! y0=sh/2
size=MIN(x0,y0)
' --- initiate graphics
GRAPHICS
GRAPHICS CLEAR 1,1,0.5
DRAW COLOR 1,0,0
DRAW SIZE 2
' --- initiate 
DRAW TO x0+a,y0
' --- loop
DO
  r=a+b*phi
  z=r*EXP(1i*phi)
  DRAW LINE TO x0+REAL(z),y0-IMAG(z)
  phi+=dphi
UNTIL ABS(z)>size
END

Please post it on Rosetta if you can

Archimedean spiral.PNG

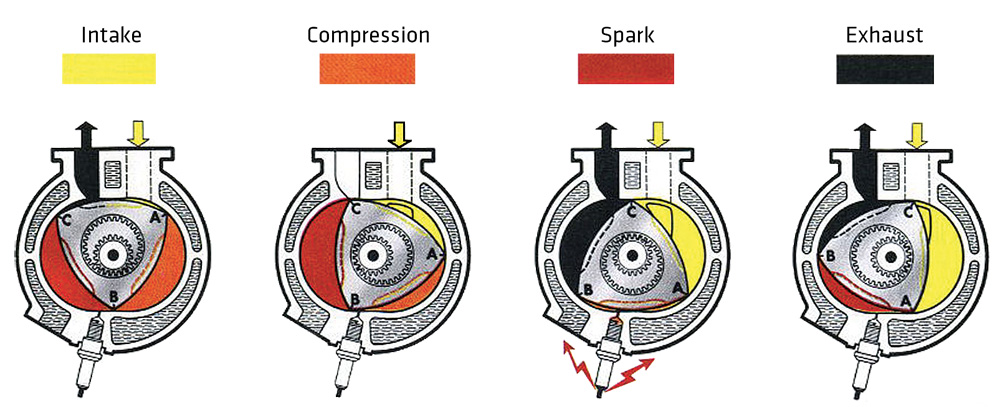
Wikipedia shows a clever application of Archimedean spirals to make a compressor. I have attached the animated gif showing a 2D cutaway of the action. One spiral is fixed, and the other rotates on an off-center axis. Imagine these two spirals as 3d shapes sealed inside a cylindrical container. Liquid or gas enters via an inlet outside the spirals. A quantity is trapped against the fixed spiral by the moving spiral on both sides simultaneously, and then pushed to the center, where it exits the container.

There is a lot more information about spirals on W.

Reminds me of a Rankle rotary engine.

Looks like the offset drive would be similar. They also have in common a lot of surface area that has to be sealed between the moving and stationary parts.